网站首页百科全书 > 正文

平衡不稳定性与稳健性：自然系统动力学的新数学框架

2024-07-29 11:18:57 百科全书来源：

导读世界各地的科学家都使用建模方法来理解复杂的自然系统，例如气候系统或神经元或生化网络。现在，一组研究人员开发了一种新的数学框架，首次...

世界各地的科学家都使用建模方法来理解复杂的自然系统，例如气候系统或神经元或生化网络。现在，一组研究人员开发了一种新的数学框架，首次解释了复杂系统中长期瞬态行为背后的机制。

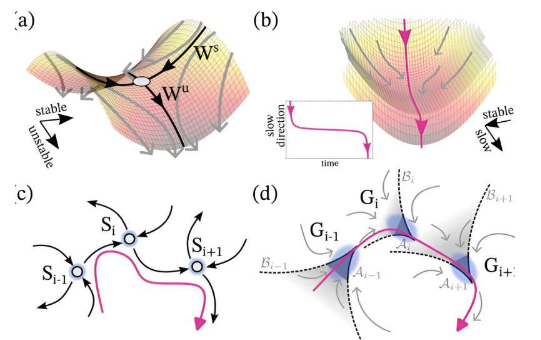
他们引入通道和循环作为新对象，解释自然系统如何能够在长时间内保持稳定，但仍然能够快速切换到另一种状态。

这种新方法挑战了基于稳定或不稳定平衡的传统概念，可能有助于我们更好地理解瞬态稳定神经元动力学如何控制感觉信息处理，或者如何潜在地预测临界级联，例如导致生物多样性丧失的级联。

马克斯普朗克行为神经生物学研究所、莱斯特大学和伦敦国王学院联合开展的这项研究成果发表在《物理评论快报》杂志上。

当你来到一个陌生的城市并询问方向时，你的工作记忆会暂时保存大量信息，例如转弯或地标，然后按照特定顺序进行作。但一旦你到达目的地，你就会忘记这些细节。为了完成这项任务，你大脑中的神经元网络具有相反的能力，既可以暂时稳定神经元活动以记住信息，也可以快速切换到序列中的不同状态。

在生态学中也可以观察到类似的动态。在竞争的微生物种群中，一个物种往往长期占主导地位，似乎定义了一种稳定的平衡，但突然之间，另一个物种毫无理由地开始接管，导致先前的物种数量减少。这种转变甚至可能导致灭绝和生物多样性丧失。

为了预测这种临界事件是否会发生以及何时发生，通常会分析转变前观察到的动态。这种预测的困难在于，它们需要事先了解状态是否确实稳定或来自长时间的瞬变，才能成功解释记录数据的统计数据。

然而，对于珊瑚礁等具有重要经济意义的生态系统，有必要确定看似健康的生态系统是否实际上可能面临陷入以藻类为主的退化状态的危险。

版权说明： 本文由用户上传，如有侵权请联系删除！

标签：